This might be a bit hard to read

Because for some reason my LATEX is not being rendered correctly. Hence, I am linking the actual paper as well.

Paper

# On the Game of Life

This was the title of a paper I was trying to get published to a math interest magazine in my college. Unfortunately they had a strict page limit (of 2 pages which is ridiculous) and though I fought for it to be changed, they never did concede. Hence, I am writing about it here!

(This is I from 2025 Jan, a year has passed and I have learnt more on the topic, however I won’t make any changes here cause I am too lazy)

# Introduction

On October 1970, Martin Gardner described the brainchild of John Conway called Life, a Cellular Automaton played on an infinite grid with no players. This paper aims to serve as a guide in this field providing some elementary mathematics behind such systems and discuss some applications of the Game of Life.

# Definitions

A Cellular Automata (CA) is a grid of uniformly arranged cells in D-dimensions, discrete in space and time where each cell encapsulates a finite value called it’s state. A State Transition Function ($\phi$) is applied to every cell, to obtain the next generation of cells. $\phi$ uses the values in the neighbourhood of a cell $X_{i,j}^t$ to determine ${X_{i,j}^{t+1}}$, where (i,j) specify the cell coordinates and t represents time (or generation).

Life uses the Moore neighbourhood, i.e. if the cell is represented by $X_{i,j}$ then the Moore neighbourhood $N_m$ of $X_{i,j}$ is $$ N_m = {X_{i-1,j-1},X_{i-1,j},X_{i-1,j+1},X_{i,j-1},X_{i,j+1},X_{i+1,j-1},X_{i+1,j},X_{i+1,j+1} }$$

In Life (no pun intended),

$$\phi = F \left(\sum_{l,m} state(N_{l,m}), state(X_{i,j}) \right)$$ and, $$ X_{i,j}^{t+1} = \phi \left( X_{i,j}^t\right)$$

Thus, a set of rules determined by $\phi$ describe the evolution of an initial state.

# Rules of Life

The cells in the Game of Life can take two values, 0 or 1 (may be thought of as alive or dead). The board in which the game is played is infinite, with all cells either living or dead, initially.

| … | 1 | 1 | 1 | 1 | 0 | … | | … | 1 | 0 | 0 | 0 | 1 | … | | … | 0 | 1 | 0 | 1 | 1 | … | | … | 1 | 1 | 0 | 0 | 0 | … |

Conway describes 3 rules that determine the next generation of cells:

1. If a live cell has less than 2 or more than 3 neighbours, it dies
2. If a live cell has 2 or 3 neighbours, it survives to the next generation
3. If a dead cell has exactly 3 neighbours, it comes back to life in the next generation

he rules can be explicitly written out as the state transition function for Life. If the current state of a cell is $S_{i,j}^t$ and the next generation is $S_{i,j}^{t+1}$ then,

$$ S_{i,j}^{t+1} = \delta \left(H_{i,j}^t,3 \right) + S_{i,j}^t \delta \left(H_{i,j}^t,2 \right) $$

where, $\delta$ is the kronecker delta function,

$$ \delta \left(a,b\right) = 1 \Longrightarrow a=b ;,; else ; 0$$

and $H_{i,j}^t$ represents the sum of the Moore neighbourhood of $S_{i,j}^t$,

$$ H_{i,j}^t = \left(\sum_{l={j-1}}^{j+1} \sum_{m={i-1}}^{i+1} S_{m,l}^t \right) - S_{i,j}^t $$

Now given an initial state of 0s and 1s, a computer can be made to apply these formulas to each cell and return the new generation.

# Example and code

Consider a finite matrix A given by:

$$A^{t=0} = $$

| 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |

Since this is a finite grid, there are 2 ways to play the Game of Life here:

1. Ignore the edges (since they do not have a well defined neighbourhood)
2. Implement a wrap-around using modulos (extend the definition of neighbours from one end to the other end of the matrix)

For the sake of this example, I will ignore the edges. Then applying the rules of Life we get the next generation,

$$A^{t=1} = $$

| 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |

You may choose to go over and verify for themselves that this indeed is in compliance with the rules.

A simple code like this one can be used to produce this system for any number of generations.

import numpy as np
from copy import deepcopy
def create_matrix(rows, columns):
    matrix = np.zeros((rows, columns), dtype = int)
    for x in range(0, columns):
        for y in range(0, rows):
            matrix[x-1][y-1] = np.random.randint(0, 2)
    return matrix
def kroneckerDelta(val1, val2):
    if val1 == val2:  return 1
    else:  return 0
def mooreSum(x,y, val):
    mooresum = 0
    for i in range(-1,2):
        for j in range(-1,2):
            mooresum += zeroDay_copy[x + i, y + j] 
    mooresum -= val
    return mooresum
def compute(x,y,val):
    assert val == 0 or val == 1; 'entered value not in base 2'
    return kroneckerDelta(mooreSum(x,y, val), 3) + val * kroneckerDelta(mooreSum(x,y, val), 2)
def life_without_boundaries(array):
    assert type(array) == np.ndarray; 'can only take numpy arrays'
    for x in range(0, columns):
        for y in range(0, rows):
            if x == 0 or x == columns-1 or y == 0 or y == rows-1: pass
            else:
                current_val = array[x,y]
                zeroDay_copy[x,y] = compute(x,y,current_val)
    return zeroDay_copy
rows = '' # put as an integer
columns = ''
zeroDay = create_matrix(rows, columns)
zeroDay_copy = deepcopy(zeroDay)
def main():
    global rows, columns, zeroDay_copy, zeroDay
    zeroDay_copy = life_without_boundaries(zeroDay)
    print(zeroDay)
    print(zeroDay_copy)
if __name__ == '__main__':
    num_gen, max_gen = 0, 10
    while num_gen <= max_gen:
        main()
        num_gen += 1

The real magic of the Game of Life is in the animations. Unfortunately it is a little hard to visualise on paper, but the reader is free to explore online.

# Applications

This is what I am most excited about. I had these ideas for a long time and even though the implementation might not go exactly as I am proposing (cause I haven’t really tried implementing that yet) its still a fun thing to ponder about.

# Hashing algorithm

Consider a number $T$ which can be represented as a binary sequence $T_{base2}$ where $length(T_{base2}$) = 1+$\lfloor log_{2}T \rfloor$. Let ${P}$ denote the set of perfect squares and $P_n$ be a perfect square such that $$ P_{n-1} < 1+\lfloor log_{2}T \rfloor \leq P_n$$ for some $n \in N$.

A salt $S$ needs to be appended to $T_{base2}$ such that $length(T_{base2}) = P_n$ because only then can it be represented in a uniform grid.

$$ length(S) = P_n - \left(1+ \lfloor log_{2}T \rfloor \right)$$

The salt is a random sequence of bits whose length is as defined above. Then, $$ T_{new} = T_{base2} \circ S $$

where $\circ$ represents concatenation. Now, consider a square matrix $A$ of dimension $\sqrt{P_n}$ whose values are bits in $T_{new}$ filled row-first.

Applying the rules of Life for $k$ generations, a new matrix $A’$ is obtained. Taking all the values row-wise and concatenating them we have a new string $T’_{base2}$ of length $P_n$.

The Game of Life is irreversible. This means it is difficult to predict the $(m-1)^{th}$ generation given the $m^{th}$ generation. The provided algorithm runs Life for $k$ generations and hence, it’s infeasible to compute the initial given the hash $T’_{base2}$. Hence, it can be implemented as a cryptographic hash function.

Prevalent cryptographic hash functions like SHA256 have a time complexity of O($n$), while Life runs at O($n^2$). However, the run-time of Life’s algorithm does not depend on the input, that is, it is always going to take the same time (more or less) to compute the hashes of two different values. Thus, it inherently prevents timing attacks.

I am not really sure how prevalent timing attacks are though!

# Proof of Work - Cryptocurrency

Cryptocurrencies achieve decentralization and sybil deterrence through what is called a ‘Proof of Work’. A group of people or computers called ‘miners’ go through the tedious task of producing some ‘unique number’ which has a special property that would validate the transaction being broadcasted.

There are 2 important properties that a valid Proof of Work must satisfy:

1. It must be require considerable effort with no better approach that brute forcing.
2. It must be easy to verify

For a grid of side 16 by 16 there exist $2^{256}$ different configurations. The following will demonstrate how Life provides a valid Proof of Work:

1. Let Alice broadcast a transaction to the world. She would take the SHA256 hash of the entire message and write that number at the end of the transaction,

2. This 256 bit binary will be encoded in a 16 by 16 grid. The transaction will be intercepted by a miner who’s purpose is to determine the starting condition for which grid appears within the $k^{th}$ generation according to the rules of Life.

3. The miner adds that starting sequence into the transaction, claims the reward and adds it to the blockchain.

Note that there is one caveat to the above, the Gardens of Eden. These are special patterns in Life that have no predecessor. The probability of the hash being a Garden of Eden is unlikely but possible.

The mining algorithm has to check all possible $2^{256}$ combinations. Checking means, the algorithm will run each combination for $k$ generations and determine if any of them match the hash. But does a unique solution exists for every transaction, given that the sequence is not a Garden of Eden?

Let M be the hash of a transaction. We can encode M in a 16 by 16 grid and apply the Life using a wrap-around. This means we map each cell on the grid to a sphere, assuring the neighbourhood $N_m$ is conserved for each cell.

Paul Erdős had shown that it is impossible to place N points on the surface of a sphere, such that they are equally spaced, except for the vertices of platonic solids. This means we have no way of mapping our 256 points on the sphere as we have no way to define $N_m$ for a cell $S_{i,j}$ if the Moore neighbourhood is not properly spaced.

The proof for the truth or falsity of the uniqueness and existence of a solution requires greater thought.

# Turing completeness

The Turing machine is a mathematical concept developed by Alan Turing. Everything algorithmically computable is computable by a Turing machine. The operation of a Turing machine is described by a State Transition Diagram (STD).

For example, consider a machine T which adds two unary numbers together, assuming they’re separated by a single 0 in between.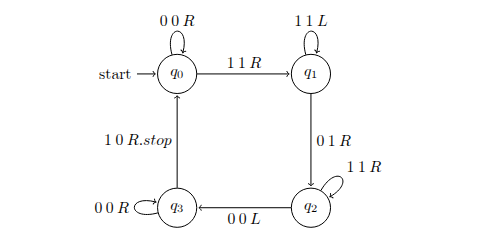

A Turing-complete machine is one that can used to solve any computational problem. An automatic machinery that can implement AND, OR and NOT gates can be combined in complex enough ways to produce a Turing-complete machine.

Conway had proved the universality of the game of life, through a special pattern called ‘glider guns’ which is used to send ‘bits’ of information. He was able to make logic gates with the glider guns and subsequently construct a system that was Turing-complete.

This has some weird consequences because now we can construct a Turing machine that would run the Game of Life, using Life (Refer to Dylan Beattie’s Art of Code).

# Conclusion

I have left a great deal to the reader like the mesmerising interplay of life and death in the game, one of the most fascinating things to watch. There are questions on whether there is an equivalence of ‘energy’ in Life, or perhaps the applicability of the $2^{nd}$ law of thermodynamics.

I hope with this short insight into Cellular Automatas the reader will be inspired to delve deeper.